How To Get The Yintercept
Understanding the Y-Intercept: A Comprehensive Guide
In the realm of mathematics, the y-intercept holds significant importance as a fundamental concept in algebra and coordinate geometry. It represents the point where a line intersects the y-axis on a Cartesian plane. This seemingly simple concept is the cornerstone for understanding linear equations, graphing lines, and analyzing relationships between variables. In this comprehensive guide, we’ll delve into the intricacies of the y-intercept, exploring its definition, calculation methods, and practical applications.
What is the Y-Intercept?
The y-intercept, often denoted as ‘b’ in the slope-intercept form of a linear equation (y = mx + b), is the value of y when x is zero. Geometrically, it’s the point where the line crosses the y-axis. This value provides crucial information about the line’s position and behavior, making it an essential component in mathematical analysis.
Methods to Calculate the Y-Intercept
There are several approaches to determining the y-intercept, each suited to different scenarios and mathematical representations.
1. Slope-Intercept Form (y = mx + b)
This is the most straightforward method when you have the equation in slope-intercept form. Here, ‘b’ directly represents the y-intercept. For instance, in the equation y = 2x + 3, the y-intercept is 3, indicating the line crosses the y-axis at the point (0, 3).
2. Rearranging Equations
If the equation is not in slope-intercept form, you can rearrange it to solve for y when x = 0. For example, given the equation 2x + 3y = 6, you can isolate y:
3y = -2x + 6 y = (-2⁄3)x + 2
Here, the y-intercept is 2.
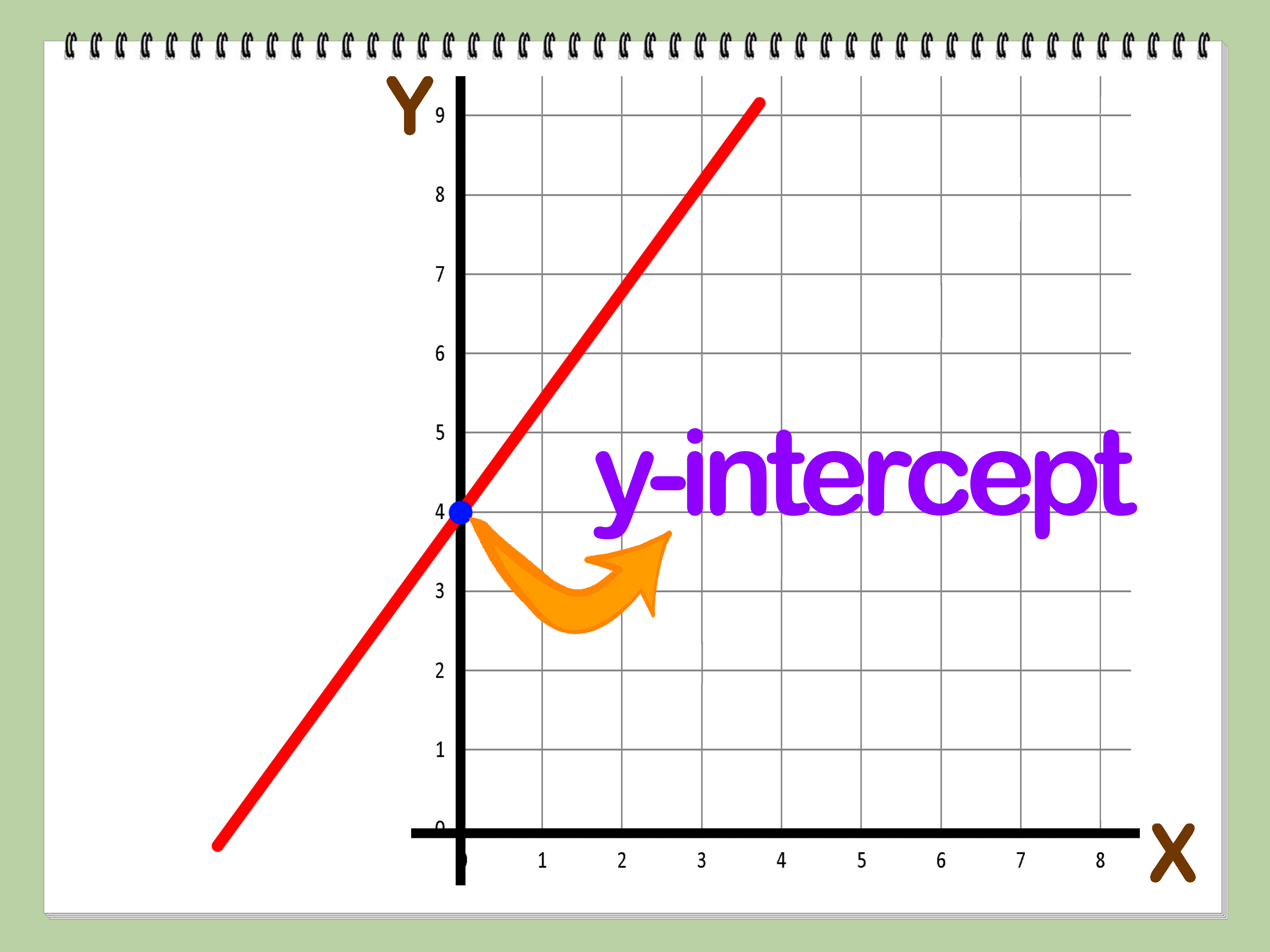
3. Graphical Interpretation
Graphically, the y-intercept is the point where the line intersects the y-axis. By plotting the line on a coordinate plane, you can visually identify the y-intercept. This method is particularly useful for verifying calculations or when dealing with non-linear equations.
4. Using Two Points (Slope Formula)
If you have two points on the line, you can calculate the slope (m) using the formula:
m = (y₂ - y₁) / (x₂ - x₁)
Then, use one of the points and the slope to find the y-intercept (b) with the slope-intercept form.
Practical Applications and Examples
Real-World Scenarios
The y-intercept is not just a theoretical concept; it has practical applications in various fields. For instance, in physics, it can represent the initial value of a quantity when time (x) is zero. In economics, it might signify the fixed cost in a cost-volume-profit analysis.
Example: Cost Analysis
Consider a company’s monthly cost equation: C(x) = 5000 + 20x, where x is the number of units produced. Here, the y-intercept (5000) represents the fixed costs, which remain constant regardless of production volume.
Comparative Analysis: Y-Intercept vs. X-Intercept
While the y-intercept focuses on the line’s intersection with the y-axis, the x-intercept is about the intersection with the x-axis. These two concepts provide different insights into a line’s behavior. The x-intercept (when y = 0) can be found by solving for x in the equation.
Common Misconceptions and Pitfalls
Myth: Y-Intercept is Always Positive
Reality: The y-intercept can be positive, negative, or zero, depending on the equation and the line’s position. For instance, y = -3x + 2 has a positive y-intercept, while y = 4x - 5 has a negative one.
Avoiding Calculation Errors
When calculating the y-intercept, ensure you correctly substitute x = 0 and simplify the equation. Common mistakes include incorrect substitution or simplifying errors, leading to inaccurate results.
Advanced Concepts: Y-Intercept in Non-Linear Equations
While this guide focuses on linear equations, the concept of intercepts extends to non-linear equations as well. In quadratic equations (y = ax^2 + bx + c), the y-intercept is still ‘c’, but the x-intercepts (roots) are found by solving the quadratic formula.
Step-by-Step Guide to Finding the Y-Intercept
Expert Insights: The Significance of Y-Intercept in Data Analysis
FAQ Section
Can the y-intercept be negative?
+Yes, the y-intercept can be negative, positive, or zero. Its sign depends on the equation and the line's position relative to the y-axis.
How do I find the y-intercept of a quadratic equation?
+In a quadratic equation (y = ax^2 + bx + c), the y-intercept is 'c'. It's the constant term, representing the point where the parabola intersects the y-axis.
What does a y-intercept of zero mean?
+A y-intercept of zero indicates that the line passes through the origin (0, 0). This means when x is zero, y is also zero.
Can I find the y-intercept without an equation?
+If you have a graph, you can visually identify the y-intercept as the point where the line crosses the y-axis. However, for precise calculations, an equation or two points on the line are typically needed.
How is the y-intercept used in real-life applications?
+The y-intercept is used in various fields, such as economics (fixed costs), physics (initial values), and data analysis (baseline predictions). It provides essential information about the behavior and position of variables.
Conclusion: Mastering the Y-Intercept
The y-intercept is a fundamental concept that serves as a gateway to understanding linear equations, graphing, and data analysis. By mastering its calculation and interpretation, you gain a powerful tool for mathematical problem-solving and real-world applications. Whether you’re a student, researcher, or professional, a solid grasp of the y-intercept is indispensable in various analytical endeavors.
In essence, the y-intercept is not just a point on a graph; it’s a key that unlocks a deeper understanding of mathematical relationships and their practical implications. As you continue your mathematical journey, remember that the y-intercept is a constant companion, offering insights and solutions across diverse disciplines.